Magic 5-gon ring
Problem 068: Magic 5-gon ring
Consider the following "magic" 3-gon ring, filled with the numbers 1 to 6, and each line adding to nine.
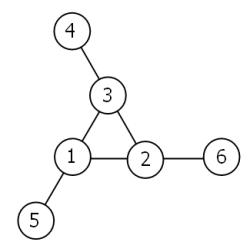
Working clockwise, and starting from the group of three with the numerically lowest external node (4,3,2 in this example), each solution can be described uniquely.
For example, the above solution can be described by the set: 4,3,2; 6,2,1; 5,1,3.
It is possible to complete the ring with four different totals: 9, 10, 11, and 12. There are eight solutions in total.
| Total | Solution Set |
|---|---|
| 9 | 4,2,3; 5,3,1; 6,1,2 |
| 9 | 4,3,2; 6,2,1; 5,1,3 |
| 10 | 2,3,5; 4,5,1; 6,1,3 |
| 10 | 2,5,3; 6,3,1; 4,1,5 |
| 11 | 1,4,6; 3,6,2; 5,2,4 |
| 11 | 1,6,4; 5,4,2; 3,2,6 |
| 12 | 1,5,6; 2,6,4; 3,4,5 |
| 12 | 1,6,5; 3,5,4; 2,4,6 |
By concatenating each group it is possible to form 9-digit strings; the maximum string for a 3-gon ring is 432621513.
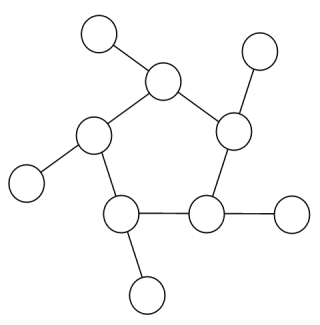
Using the numbers 1 to 10, and depending on arrangements, it is possible to form 16- and 17-digit strings. What is the maximum 16-digit string for a "magic" 5-gon ring?
Solution:
X OOOOOOOOOO
>":"v v < <
v < vp1+9-"0"g0+9p03:-1g03"O" <
>90p030p>30g9+0g1-:30g9+0p"0"-:70p0\`|
v g03_^#! -"O"g1+9g07 #<$
>:#v_70g5` >|
v-1< v _v#!`g039$ <
>:#v_ 70g9-! ^
v-1< >"X"70g9+1p":"30g1+:30p9+0p^
>:#v_ 90+0g91+0g92+0g++51p70g9-! ^
v-1< >91+0g"/"- 98+0g"/"- 99+0g"/"- v
>:#v_90g"0"-70g` ^
v-1< v-"/"g0+79 -"/"g0+69 -"/"g0+89 <
>:#v_ 92+0g93+0g94+0g++51g-!!70g9-!+ ^
v-1< >96+0g"/"- 94+0g"/"- 95+0g"/"- v
>:#v_90g"0"-70g` ^
v-1< v-"/"g0+39 -"/"g0+29 -"/"g0+49 <
>:#v_ 94+0g95+0g96+0g++51g-!!70g9-!+ ^
v-1< >92+0g"/"- 91+0g"/"- 90+0g"/"- v
>:#v_90g"0"-70g` ^
v-1< @ ... ... ... ... ...<
>:#v_96+0g97+0g98+0g++51g-!!70g9-!+ ^
v89<
>+0g99+0g91+0g++51g-!!90g"0"-70g`!!+ ^
Explanation:
The solution to this problem is similar to problem-043. We iterate through all possible 10-digit combinations but abort most paths pretty early through a few rules. This leads to a pretty quick execution time an a not so big program.
I even managed to squeeze all in only half the available width so the other half has space enough for an ASCII representation of the magic 5-gon ring :D.
(You can see the result in the problem-068 (visual) file)
The main piece (excluding the act of pressing everything in such a small space) was formulating the rules. The more (an the earlier triggering) rules, the less paths we have to traverse and the faster our program gets: (I needed to index the elements of the ring, so I went clockwise from the outermost to the inner elements.
The rules are:
N_3 > N_0,N_5 > N_0,N_7 > N_0,N_9 > N_0. We wantN_0to be the smallest element to avoid getting the same solution multiple times, only rotated. (Also it is stated that we start counting from the smallest outer element)N_0 <= 5, otherwise it can't be the smallest outer elementN_1 <> 9,N_2 <> 9,N_4 <> 9,N_6 <> 9,N_8 <> 9, otherwise we won't get an 16-digit numberN_2+N_3+N_4 = N_0+N_1+N_2,N_4+N_5+N_6 = N_0+N_1+N_2,N_6+N_7+N_8 = N_0+N_1+N_2,N_8+N_9+N_1 = N_0+N_1+N_2. Our condition for the ring to be "magic"
| Interpreter steps: | 304 112 |
| Execution time (BefunExec): | 78ms (3.90 MHz) |
| Program size: | 39 x 25 (fully conform befunge-93) |
| Solution: | 6531031914842725 |
| Solved at: | 2015-07-16 |

