Right triangles with integer coordinates
Problem 091: Right triangles with integer coordinates
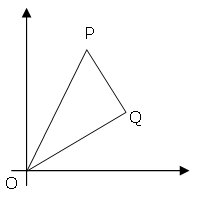
The points P(x1, y1) and Q(x2, y2) are plotted at integer co-ordinates and are joined to the origin,
O(0,0), to form OPQ.
There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is,
0 <= x1, y1, x2, y2 <= 2.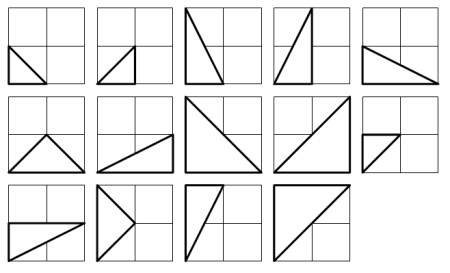
Given that 0 <= x1, y1, x2, y2 <= 50, how many right triangles can be formed?
Solution:
X XXXX >$41p#^_31g311g:**+.@>$p v1+
>1g51g:61g-\*41g%!2*+31p61g1+61pv!56
^ >51g#^ #:1# - #1:#g5#11#4 ^# _^1
^3_^#! +`g11g16`*:g14*-\g16:g15< p<
Explanation:
This was mostly a mathematical problem.
Lets go step by step through my solution:
We have a triangle with three corners, O(o_x, o_y), Q(q_x, q_y) and P(p_x, p_y), where O = (0,0).
We can quickly see that there are three types of solutions, triangles where O has the right angle,
triangles where Q has the right angle and triangles where P has the right angle.
The amount of triangles in group two (angle at Q) and group three (angle at P) are identical (!)
Because for every triangle in group two there is a triangle in group three which has the points P and Q mirrored at the vertical Axis (1, 1).
So when we have a triangle O(0, 0); Q1(q1_x, q1_y); P(p1_x, p1_y) the corresponding mirrored triangle is
q2_x = q1_y
q2_y = q1_x
p2_x = p1_y
p2_y = p1_xThese two groups (two and three) are also mutually exclusive, because if Q1 == P2 and Q2 == P1 then the vectors OP and OQ would have equal length and
the only possible right angle could be at point O (and not at P or Q).
Now that we have proven that count(group_2) == count(group_3) we only have to find that triangle count and the amount of triangles in group one.
First group one:
To have an right angle at the zero point O(0, 0) both other points have to lie on an axis.
We say point Q lies on the x-axis and point P on the Y-axis. All combinations lead to valid and unique triangles, the only disallowed point is the origin (0, 0).
So we have SIZE possible positions on the x-axis and SIZE possible positions on the y-axis. This leads to SIZE * SIZE different unique triangles:
count(group_1) = SIZE * SIZENow group 2/3
Because we need to define a bit of semantics we say our point Q is the lower-right point of the triangle (and P is the upper left),
similar to the project-euler example image. Also we want our right angle to be at point Q (between the vectors OP and PQ).
First we can look at the trivial triangles, the ones where Q lies on the x-axis and P has the same x-coordinate as Q.
These triangles all have an right angle at Q and are valid solutions. And because there are SIZE possible positions for Q (all x-axis positions except (0,0))
and for each of these there are SIZE possible positions for P (all points on the same x-value as Q, except y = 0)
there are SIZE*SIZE trivial triangles with an right angle at Q.
count(group_2_triv) = count(group_3_triv) = SIZE * SIZEFor the remaining triangle we can finally - kind of - start programming.
We go through all remaining points (q_x, q_y) where q_x > 0 && q_y > 0 (because the axis are already covered by our trivial cases).
For every point (that we assume is Q) we calculate the vector OQ:
oq_x = q_x - 0 // trivial, yeah i know. In the final program this is all optimized away
oq_y = q_y - 0And we calculate the direction of the vector QP (under the assumption that Q has a right angle and thus OQ and QP form a right angle). This is simply the vector OQ rotate by 90° CW:
v_qp_x = -oq_y;
v_qp_y = oq_x;Now we search for integer solutions of P = Q + n * v_QP. Each solution, that also falls in our SIZE bounds is a valid triangle.
To find these we go through all the possible y locations out point P can have.
It is not possible that one p_y value responds to multiple p_x values, because then QP would be horizontal
and these triangles are already acknowledged in our trivial cases of group_2 / group_3.
So for each (possibly valid) p_y value we can calculate the corresponding p_x value:
p_y = q_y + n * v_qp_y
n = (p_y - q_y) / v_qp_y
p_x = q_x + n * v_qp_x
= q_x + ((p_y - q_y) / v_qp_y) * v_qp_x
= q_x + ((p_y - q_y) * v_qp_x / v_qp_y)First we want to test if (p_y - q_y) * v_qp_x is a multiple of v_qp_y.
If this were not the case than p_x is not an integer and this is not an integer solution
(then we would simply continue with the next y value until y > SIZE and we have reached our limit).
But if P(p_x, p_y) has two integer components we only need to test if p_x is greater than zero
(because otherwise the triangle would be out of our defined bounds) and then we can increment out triangle counter.
Be aware that we have in this step practically found two unique triangles, this one and its mirrored counter part (see explanation at the beginning).
Now we continue our looping, first until we have tested all possible p_y values (until p_y grows greater than our bounds, SIZE)
and then until we have tested all valid points for Q.
In the end we only have to add our values together and we have our result:
result = c_group_1 + 2 * c_group_23
c_group_23 = c_group_23_triv + c_group_23_nontrivThis is one of the problems that translate really well into befunge, because there are no big data structures and not even a lot of calculations. Most of the work is done before we start to write code and the challenge is finding the correct approach.
After note: I really want a price or something for the compression of this program. Everything is crunched into a 36x5 rectangle and there are nearly no unused codepoints...
| Interpreter steps: | 3 072 923 |
| Execution time (BefunExec): | 343ms (8.96 MHz) |
| Program size: | 36 x 5 (fully conform befunge-93) |
| Solution: | 14234 |
| Solved at: | 2016-05-26 |

