Counting rectangles
Problem 085: Counting rectangles
By counting carefully it can be seen that a rectangular grid measuring 3 by 2 contains eighteen rectangles:
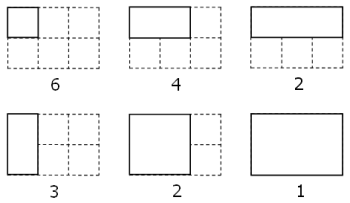
Although there exists no rectangular grid that contains exactly two million rectangles, find the area of the grid with the nearest solution.
Solution:
YY YY YY
>"}}_!"+**:10p11p051p071p>10g71g`v
v*`g18g01`g14g15<p18 g17p141_v
v8g01_51g1+:51p71g+7 1p^ @.g12<
>1g-:0\`#v_0>-:11g`#v_11p41g5v
>*81g+81v>0\^v+1g14$<#0p12*g1<
^g17p14:># p#< ^
Explanation:
The key to solve this problem is effectively iterating through the permutations for a given width and height (perms[w, h]).
First we look at the baseline with width=1. The basic case perms[1,1] is 1.
After that perms[1,h] = perms[1,h-1] + h (so we can iterate easily through all these solutions).
With the baseline in place we can see that perms[w, h] = perms[w, h-1] + perms[w, 1] * h.
Then we just iterate through all the possibilities and search for the smallest difference.
We can stop increasing the width when perms[w, 1] > 2,000,000 and similar stop increasing the height when perms[w, h] > 2,000,000 or w > h.
The second conditions stems from the fact that perms[w, h] == perms[h, w] (it's a mirrored functions).
Through these limiting conditions and the fact that each step is pretty fast (just a few additions and multiplications) this algorithm is really fast. (We only test around 10000 values before our search space is depleted)
| Interpreter steps: | 880 151 |
| Execution time (BefunExec): | 109ms (8.07 MHz) |
| Program size: | 35 x 8 (fully conform befunge-93) |
| Solution: | 2772 |
| Solved at: | 2015-10-03 |

